Modelling an Equation for Forward Speeds of a Ring

By Bhanaviya and Ben

Task: Model a projectile motion equation to approximate forward speeds of rings launched from a ring launcher

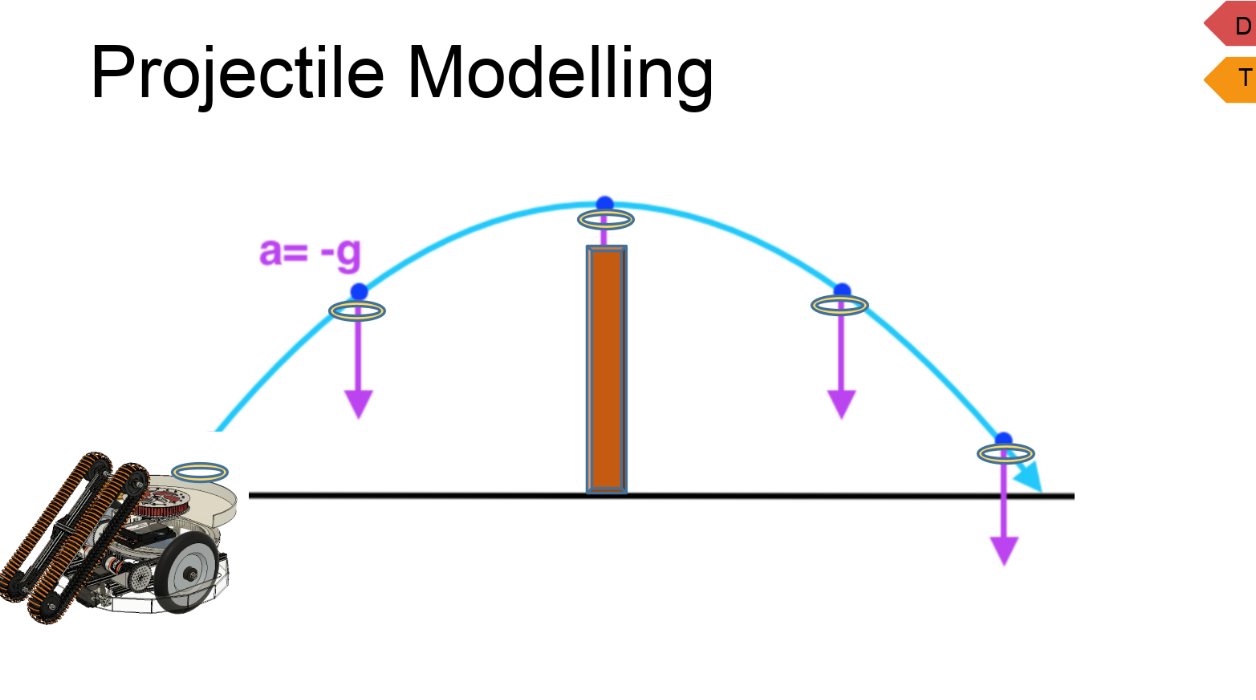
A key challenge in this year's game is finding the best possible position to launch rings to ensure optimal performance of the ring launchers. Part of this challenge includes approximating a potential forward speed for each ring as it is launched from the launcher itself. There was also height and distance constraints that needed to be taken into account before we could find these forward speeds. Modelling an equation to identify this forward speed would allow us to directly plug in this equation into the robot's code so it can automatically adjust itself to aim rings from an optimal angle and position.

In order to find the most optimal position and angle to launch the rings, we needed to first consider the angle of the launcher to be a variable to determine all possible forward speeds horizontally and vertically. We needed to look at the forward speeds both vertically and horizontally in order to attain the maximum distance (which would be tangential to the horizontal and vertical distance if we were to look at it like a right triangle). FTC constraints dictate that the maximum height a ring can be launched was 16ft we translated to 4.85 meters. While this was not a contant we inputted into our formulas, it was something for us to consider when we began. We knew that the height of our robot with the shooter mounted was roughly 0.41m and aiming to get the ring into the third level of the goals, we knew that the height the ring needed to reach was 0.88m. Subtracting the desired height from the initial height, we got 0.47m, and by placing that on one side of our projectile equation, we used simple algebra to find out that to isolate v0, 1/2(-a)t^2 needed to be subtracted from 0.47m for the vertical velocity. Since the final horizontal distance varies from launch to launch, we left it as xF (final horizontal distance) - 0 (inital horizontal distance) to reflect our steps for the vertical equation.

When we began planning our equation, there were 3 things we anticipated we needed to know. 1) Angle of launch - this was what we were intending to find but we wanted a formula so we wouldn't have to manually measure theta each time. 2) Initial vertical speed - this was another unknown which affected the distance our rings could travel, which, consequently, relied on the measure of the angles. Finally 3) time - there are two things we need to know about time. First, how long the ring stays in the air, and second how long it takes for the ring to reach zero vertical velocity (in other words, when does it reach its maximum height?) Another issue we needed to account for was how the end of our equation would be represented. Did we want the height of the third level goal to be the summit of the ring's arc or did we want it to be its final point? Since we knew that the ring were not being launched 0 meters away from the ground but rather 0.41 meters away, aiming for the goal to be the end of its arc past its apex would cause too much error in our model if we were to graph the ring's arc as a parabola. So, we settled for making the summit of our parabola be the third level of the goal. So, time in our equation was represented as t/2 since in a standard parametric equation, t for time represents the complete arc while t/2 cuts the arc off at the apex. With all this taken into account, we were able to model two different equations - one for the horizontal velocity of the ring and second for the vertical velocity of the ring.

Our equations were: Vertical: v0 = (0.47 - 0.5(-a)(t^2))/sinθ(t/2)) and Horizontal: v0 = (xF - 0.5(-a)(t^2))/cosθ (t/2)) t stands for time in seconds, a for acceleration due to gravity - 9.8 m/s^2 and xF for the final horizontal distance of the robot which will be calculated by the robot itself.

While having two unknowns in our equation in a concern, we plan to find the velocity of one, plug it into the equation for the other side and retrieve theta from there. We want theta to be the same for both the horizontal and vertical equation assuming that the distance they travel is the same.

Next Steps

The next step would be for us to plug in constants into our equations and check to see if the velocity and theta seem to be reasonable. We anticipate that these equations will undergo several changes as we continue to build the ring launcher. Even once the equation is finalized, we will need to figure out how to translate it into code and whether or not we can find values such as RPM and muzzle velocity in order to control our motor to provide us our desired launch.