Adding Margins Of Error To Desmos

By Mahesh

Task: Add Margins Of Error To The Desmos Calculator

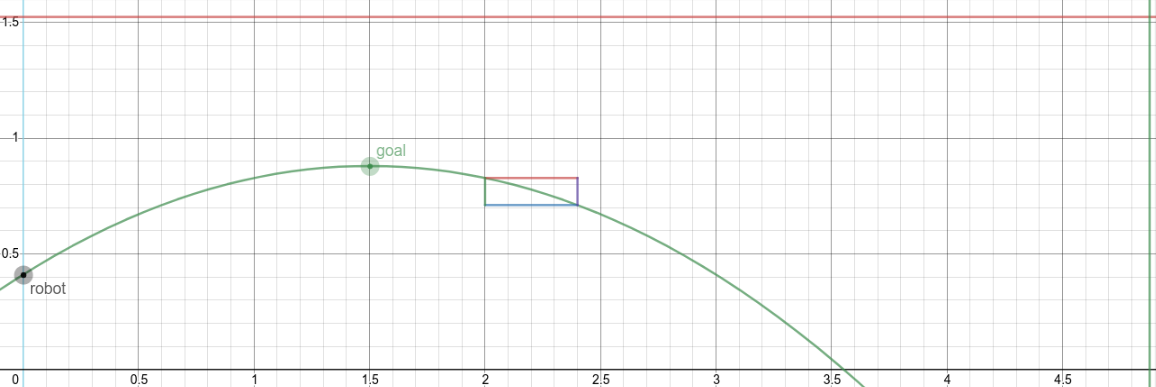
In order to visually represent the significance of placing the constraints we did, we modified our desmos trajectory calculator to include a margin of error box. This box would help to highlight the importance of keeping the summit of our trajectory aligned with the goal, and how deviations from the summit would result in drastically increasing margins of vertical error for the same horizontal error.

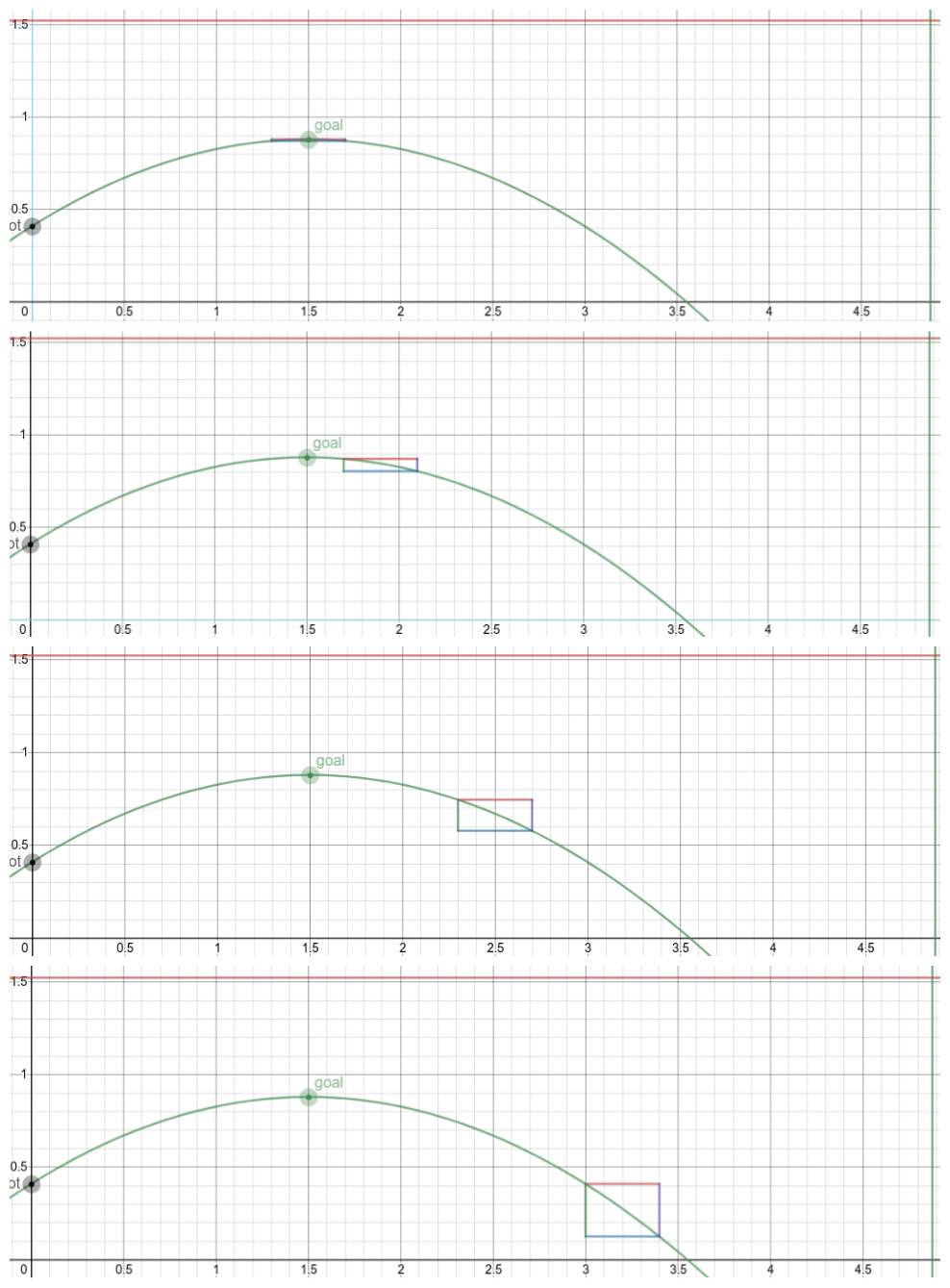
As seen above, even with the same theoretical horizontal margin of error, having the goal (which can be thought of as the center of the error rectangle) placed further from the summit of the trajectory results in a larger vertical error. This helps to visually justify why we chose to have the summit of the disk's trajectory at the height of the goal, because the disk's vertical margin of error is minimized with that constraint.

Additionally, we are able to minimize the energy required to launch the disk. This is because, by the law of conservation of energy, the energy at any point in the disk's launch must be equal to the energy at any other point. We can consider the point where the disk is about to be launched from the launcher and the point where the disk is at it's maximum height. The total mechanical energy (kinetic energy + gravitational potential energy) of the disk in these two points must be equal.

Kinetic energy is represented by \[\displaylines{K = \frac{1}{2}mv^2}\]

and gravitational potential energy is represented by \[\displaylines{U_g = mgh}\]

The higher the disk goes, the larger the total mechanical energy of the disk at the highest point in it's trajectory, since \(U_g\) is proportional to \(h\). And by the laws of conservation of energy, the energy at the start of the launch would have to equal this larger mechanical energy for the disk to reach a higher altitude. By having the disk only go as high as it needs to in order to reach the goal, we minimize the total energy we need to put into the disk and the initial velocity of the disk at launch (since \(K\) is proportional to \(v^2\)). This is ideal for our flywheel as the likelihood of it being not fast enough is minimized.

The link to the edited desmos calculator can be found at https://www.desmos.com/calculator/csxhdfadtm, with \(E_c\) being the variable to control the center of the error rectangle and \(E\) being the variable to control the margin of horizontal error.