08 Dec 2021
Post 54
Awards: think and control
Deriving Inverse Kinematics For The Drivetrain
By Mahesh, Cooper, and Ben
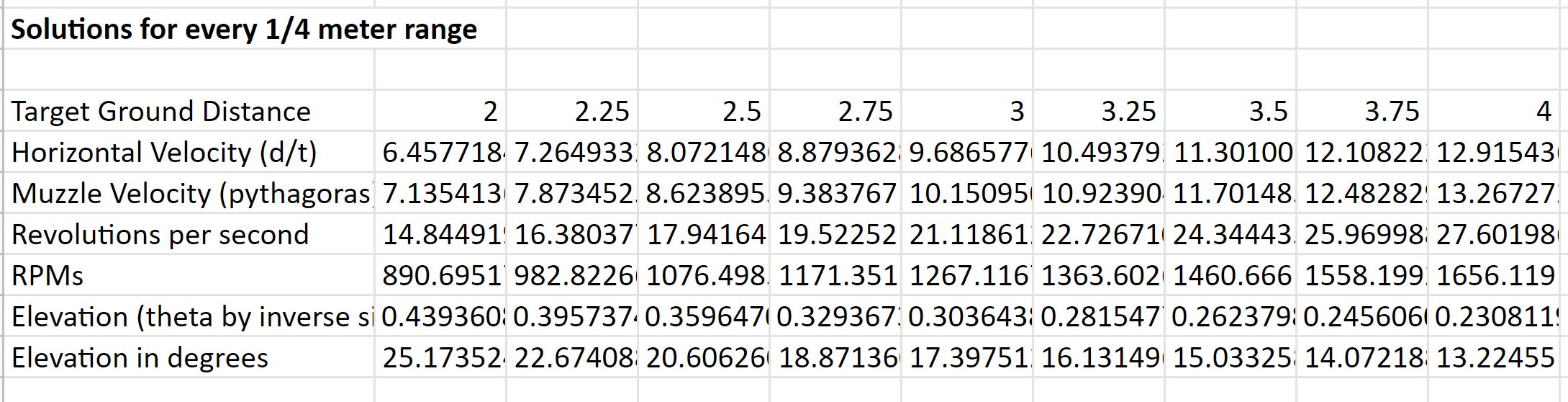
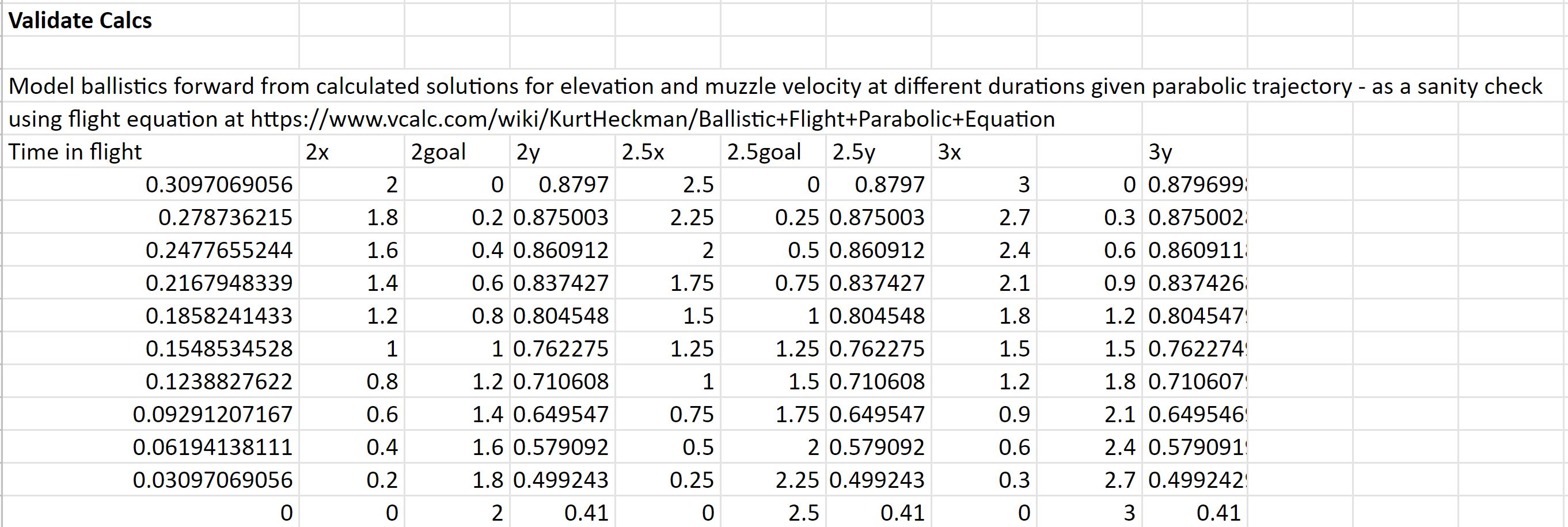
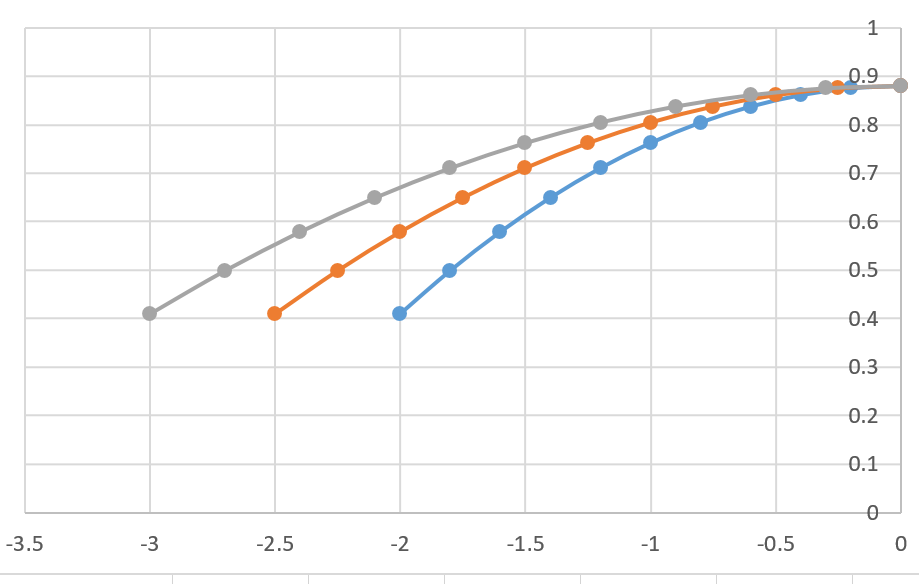
Task: Derive Inverse Kinematics For The Drivetrain
Due to having an unconventential drivetrain consisting of two differental
wheels and a third swerve wheel, it is crucial that we derive the inverse
wheel kinematics early on. These inverse kinematics would convert a
desired linear and angular velocity of the robot to individual wheel
velocities and an angle for the back swerve wheel. Not only would these
inverse kinematics be used during Tele-Op to control the robot through
joystick movements, but it will be useful for getting the robot to travel
at a desired forward velocity and turning rate for autonomous path
following. Either way, deriving basic inverse kinematics for the
drivetrain is a necessity prerequisite for most future programming
endeavors.
More concretely, the problem consists of the following:
Given a desired linear velocity \(v\) and turning rate/angular velocity
\(\omega\), compute the required wheel velocities \(v_l\), \(v_r\), and
\(v_s\), as well as the required swerve wheel angle \(\theta\) to produce
the given inputs. We will define \(v_l\) as the velocity of the left
wheel, \(v_r\) as the velocity of the right wheel, and \(v_s\) as the
velocity of the swerve wheel.
To begin, we can consider the problem from the perspective of the robot
turning with a given turning radius \(r\) with tangent velocity \(v\).
From the equation \(v = \omega r\), we can conclude that \(r =
\frac{v}{\omega}\). Notice that this means when \(\omega = 0\), the radius
blows up to infinity. Intuitively, this makes sense, as traveling in a
straight line (\(\omega = 0\)) is equivalent to turning with an infinite
radius.
The main equation used for inverse wheel kinematics is:
\[\displaylines{\vec{v_b} = \vec{v_a} + \vec{\omega_a} \times \vec{r}}\]
Where \(\vec{v_b}\) is the velocity at a point B, \(\vec{v_a}\) is the
velocity vector at a point A, \(\vec{\omega_a}\) is the angular velocity
vector at A, and \(\vec{r}\) is the distance vector pointing from A to B.
The angular velocity vector will point out from the 2-D plane of the robot
in the third, \(\hat{k}\), axis (provable using the right-hand rule).
But why exactly does this equation work? What connection does the cross
product have with deriving inverse kinematics? In the following section,
the above equation will be proven. See section 1.1 to skip past the proof.
To understand the equation, we start by considering a point A rotating
around aother point B with turn radius vector \(\hat{r}\) and tangent
velocity \(\vec{v}\).
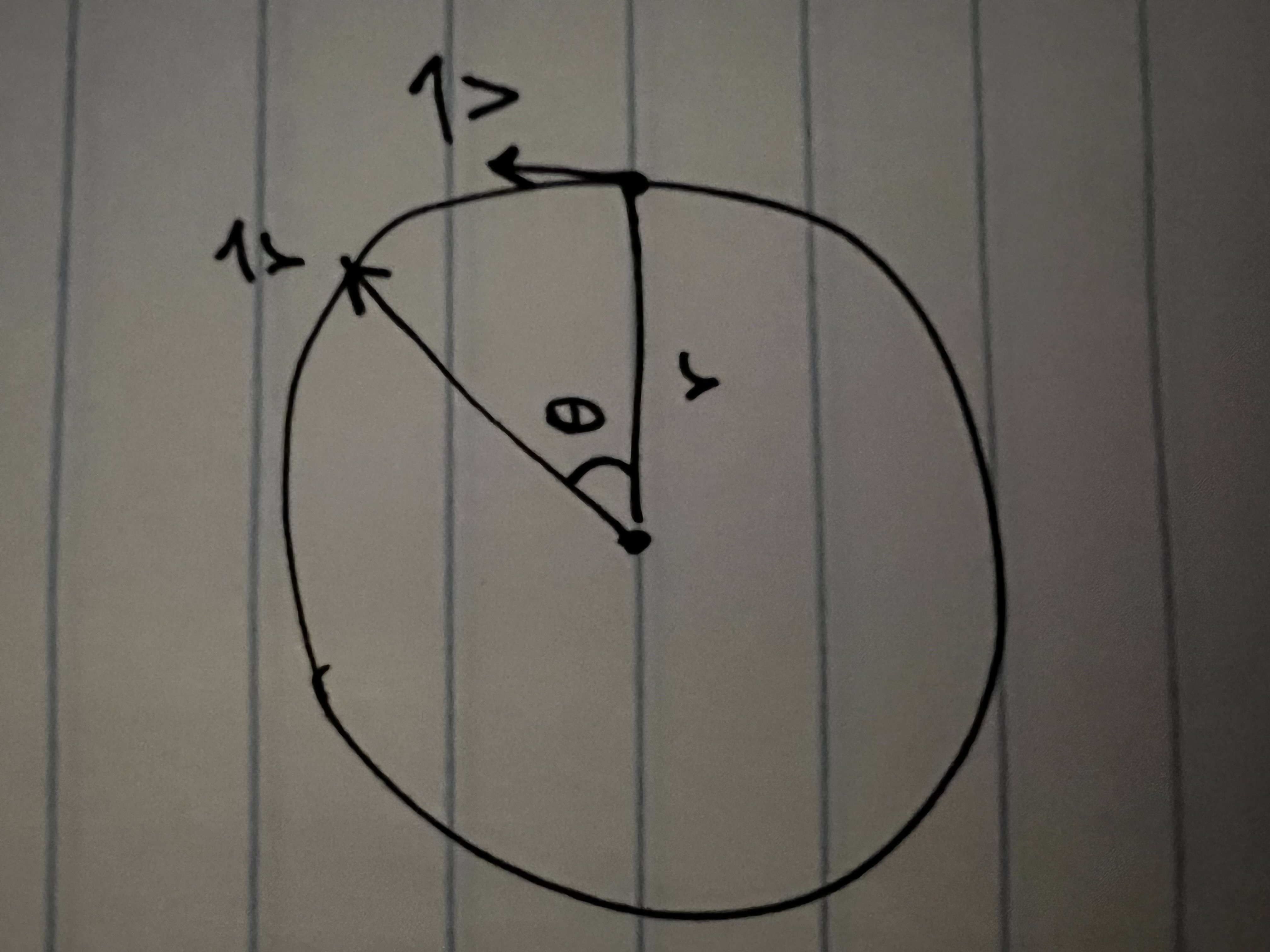
For an angle \(\theta\) around the x-axis, the position vector \(\vec{s}\)
can be defined as the following:
\[\displaylines{\vec{s} = r(\hat{i}\cos\theta + \hat{j}\sin\theta) }\]
by splitting the radius vector into its components and recombining them.
To arrive at a desired equation for \(\vec{v}\), we will have to
differentiate \(\vec{r}\) with respect to time. By the chain rule:
\[\displaylines{\vec{v} = \frac{d\vec{s}}{dt} = \frac{d\vec{s}}{d\theta}
\cdot \frac{d\theta}{dt}}\]
The appropriate equations for \(\frac{d\vec{s}}{d\theta}\) and
\(\frac{d\theta}{dt}\) can then be multiplied to produce the desired
\(\vec{v}\):
\[\displaylines{\frac{d\vec{s}}{d\theta} = \frac{d}{d\theta} \vec{s} =
\frac{d}{d\theta} r(\hat{i}\cos\theta + \hat{j}\sin\theta) =
r(-\hat{i}sin\theta + \hat{j}cos\theta) \\ \frac{d\theta}{dt} = \omega \\
\vec{v} = \frac{d\vec{s}}{dt} = \frac{d\vec{s}}{d\theta} \cdot
\frac{d\theta}{dt} = r(-\hat{i}sin\theta + \hat{j}cos\theta) \cdot \omega
\mathbf{= \omega r(-\hat{i}sin\theta + \hat{j}cos\theta)} }\]
Now that we have an equation for \(\vec{v}\) defined in terms of
\(\omega\), \(r\), and \(\theta\), if we can derive the same formula using
\(\vec{\omega} \times \vec{r}\), we will have proved that \(\vec{v} =
\frac{d\vec{s}}{dt} = \vec{\omega} \times \vec{r}\)
To begin, we will define the following \(\vec{\omega}\) and \(\vec{r}\):
\[\displaylines{ \vec{\omega} = \omega \hat{k} = \begin{bmatrix}0 & 0 &
\omega\end{bmatrix} \\ \vec{r} = r(\hat{i}cos\theta + \hat{j}sin\theta) =
\hat{i}rcos\theta + \hat{j}rsin\theta = \begin{bmatrix}rcos\theta &
rsin\theta & 0\end{bmatrix} }\]
Then, by the definition of a cross product:
\[\displaylines{ \vec{\omega} \times \vec{r} = \begin{vmatrix} \hat{i} &
\hat{j} & \hat{k} \\ 0 & 0 & \omega \\ rcos\theta & rsin\theta & 0
\end{vmatrix} \\ = \hat{i}\begin{vmatrix} 0 & \omega \\ rsin\theta &
0\end{vmatrix} - \hat{j}\begin{vmatrix} 0 & \omega \\ rcos\theta &
0\end{vmatrix} + \hat{k}\begin{vmatrix} 0 & 0 \\ rcos\theta &
rsin\theta\end{vmatrix} \\ = \hat{i}(-\omega rsin\theta) - \hat{j}(-\omega
rcos\theta) + \hat{k}(0) \\ \mathbf{= \omega r(-\hat{i}sin\theta +
\hat{j}cos\theta)}}\]
Since the same resulting equation, \(\omega r(-\hat{i}sin\theta +
\hat{j}cos\theta)\), is produced from evaluating the cross product of
\(\vec{\omega}\) and \(\vec{r}\) and by evaluating
\(\frac{d\vec{s}}{dt}\), we can conclude that \(\vec{v} = \vec{\omega}
\times \vec{r}\)
1.1
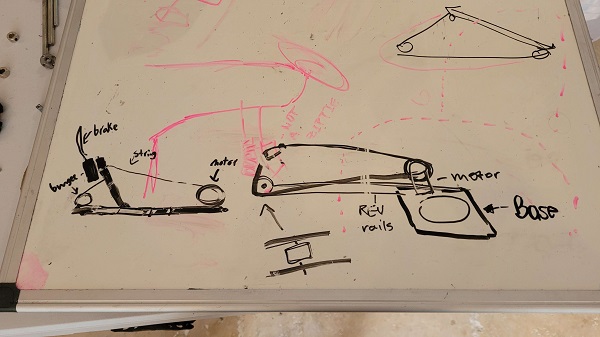
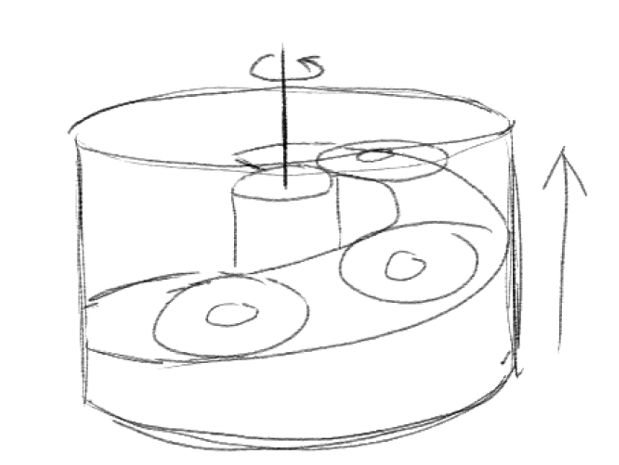
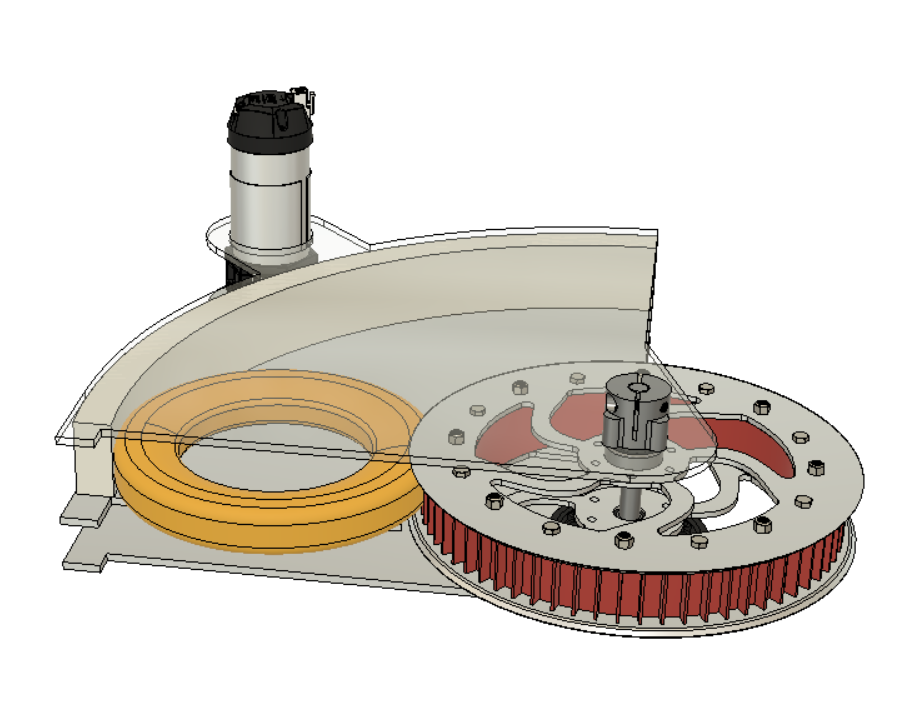
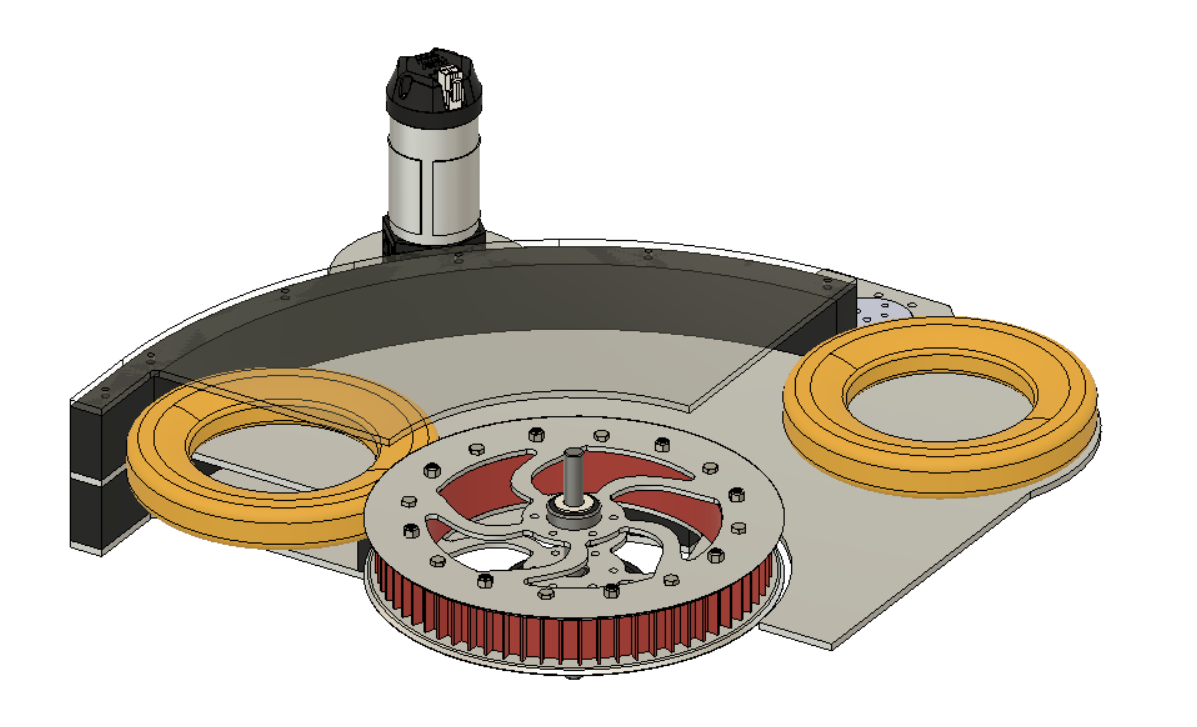
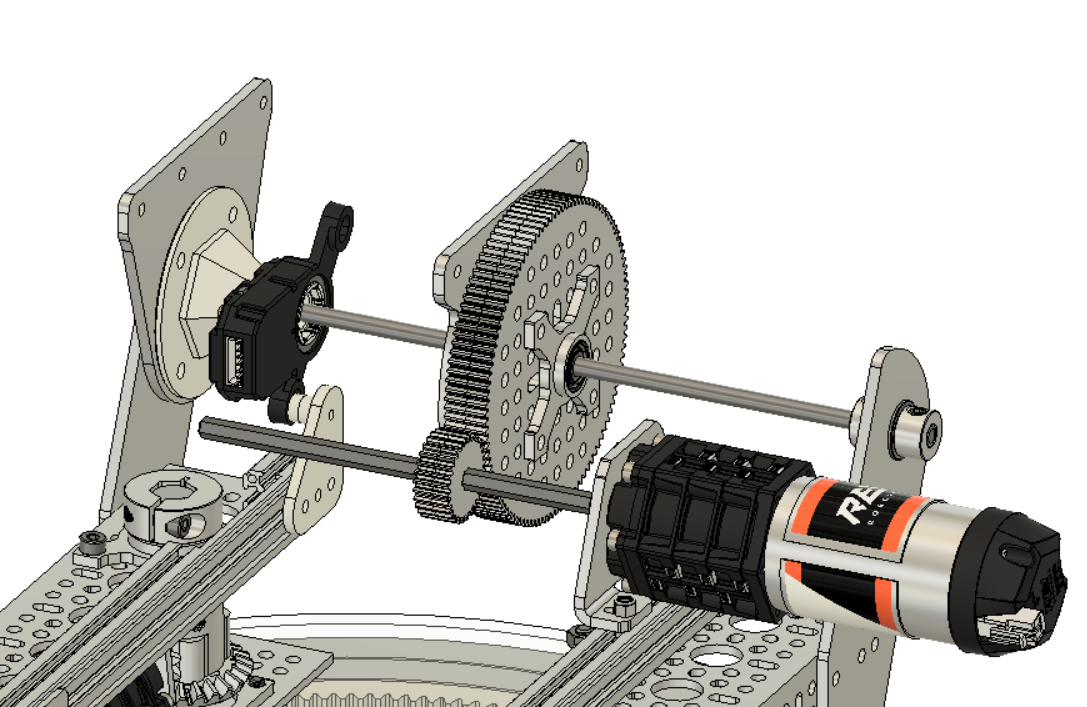
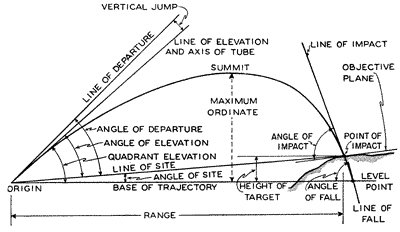
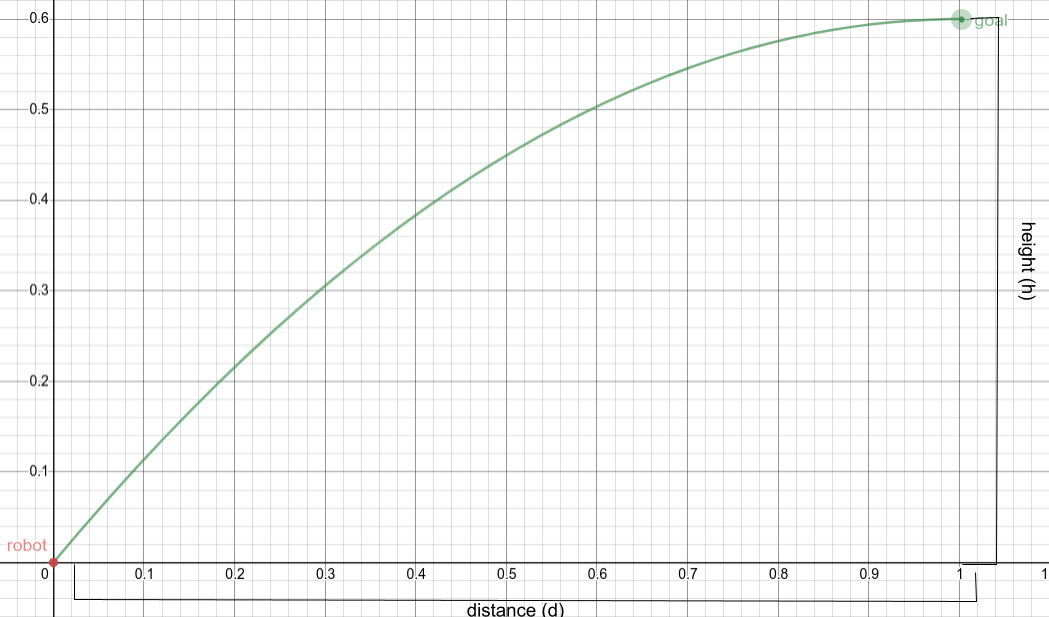
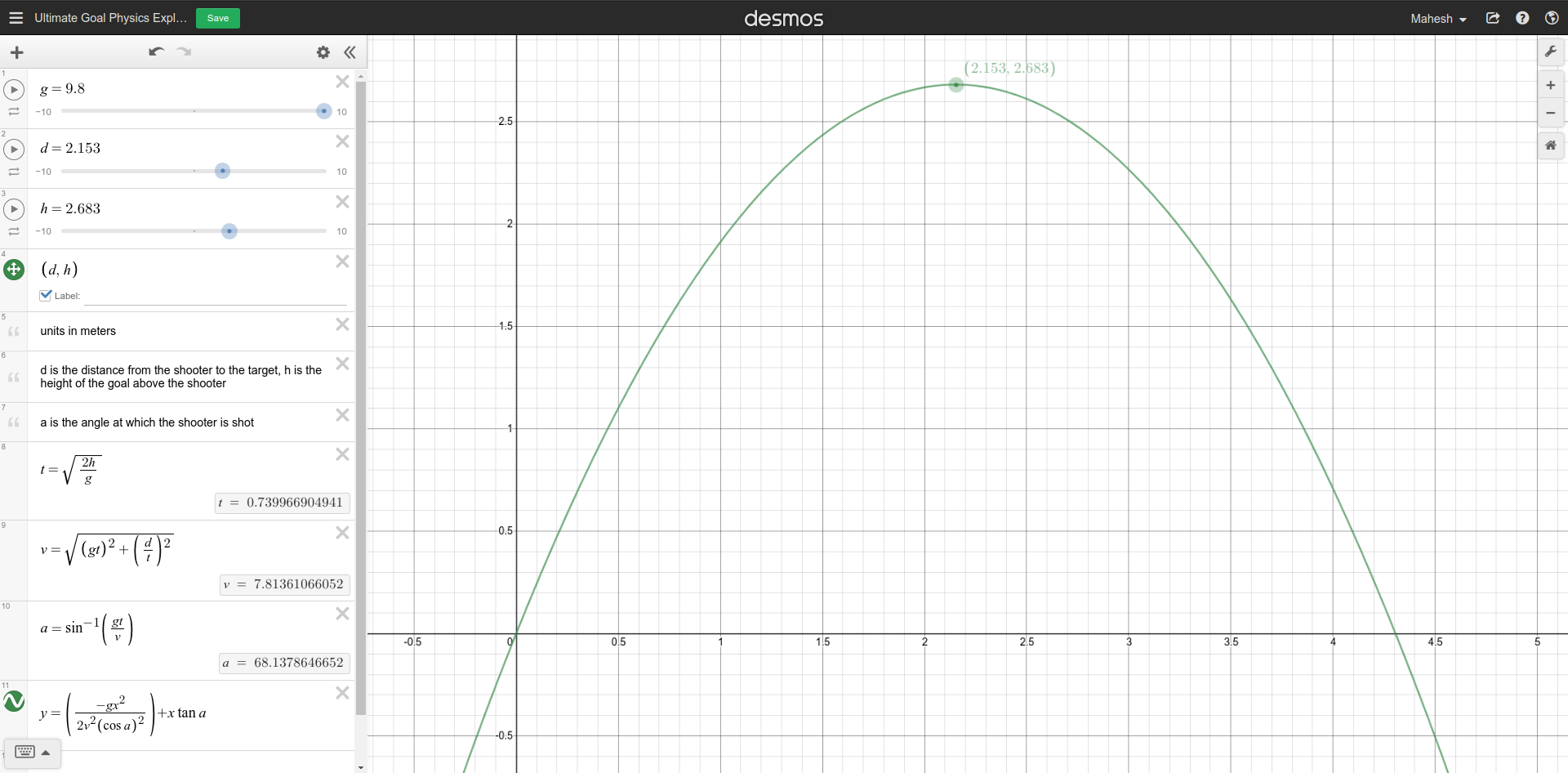
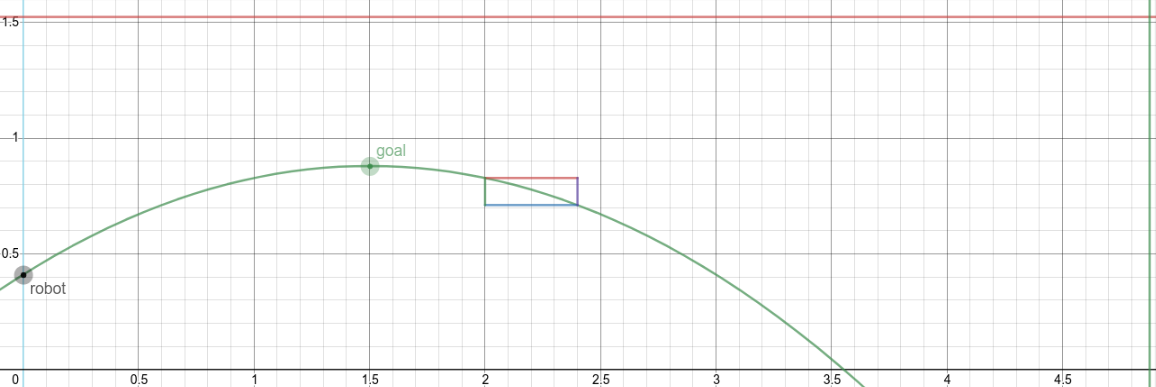
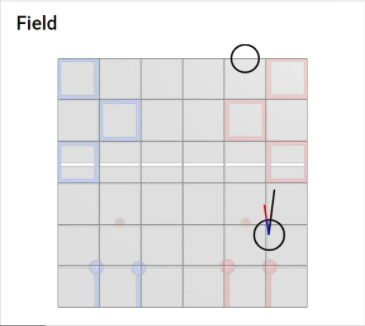
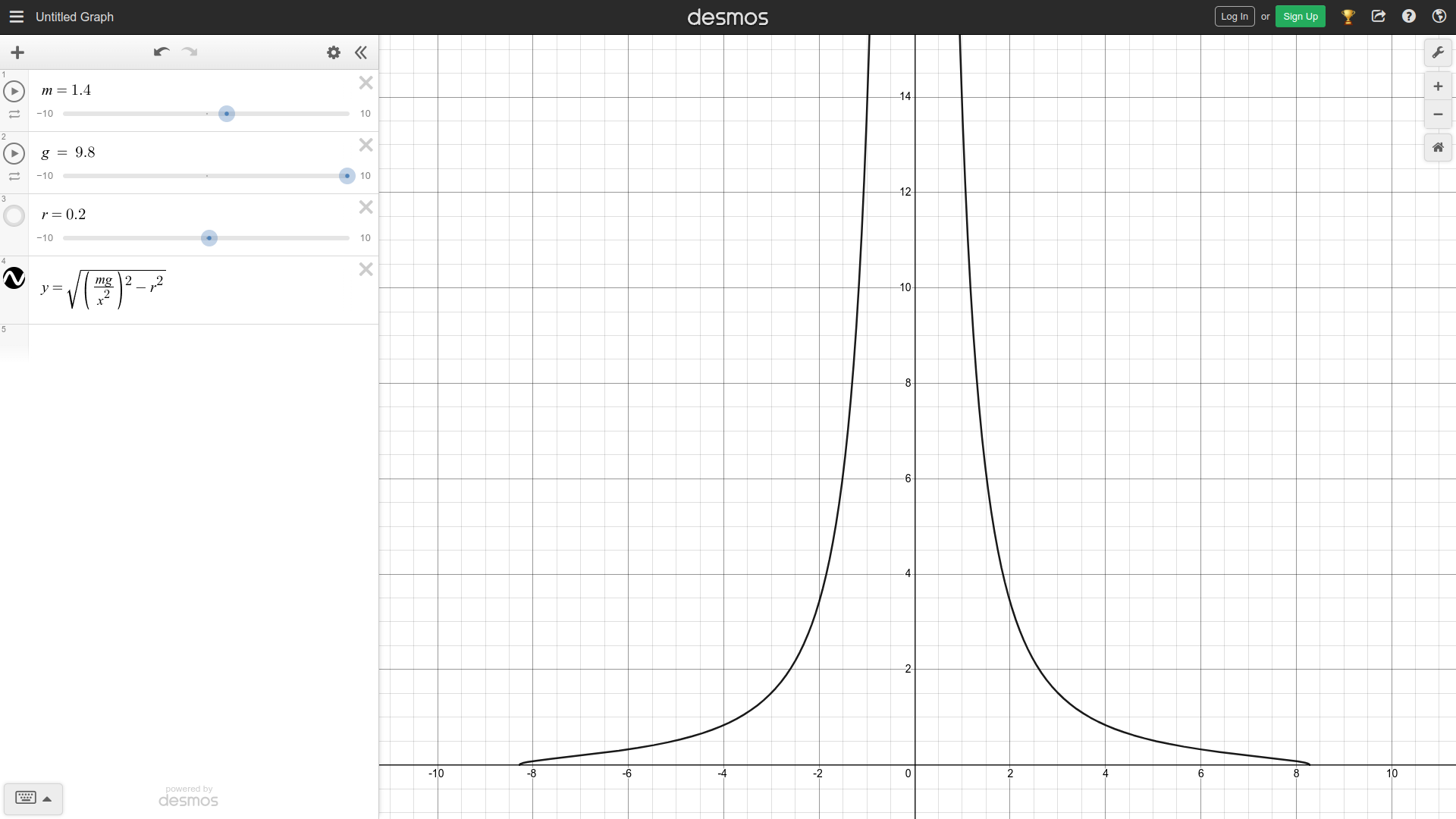
Based on the constants defined and geometry defined in the image below:
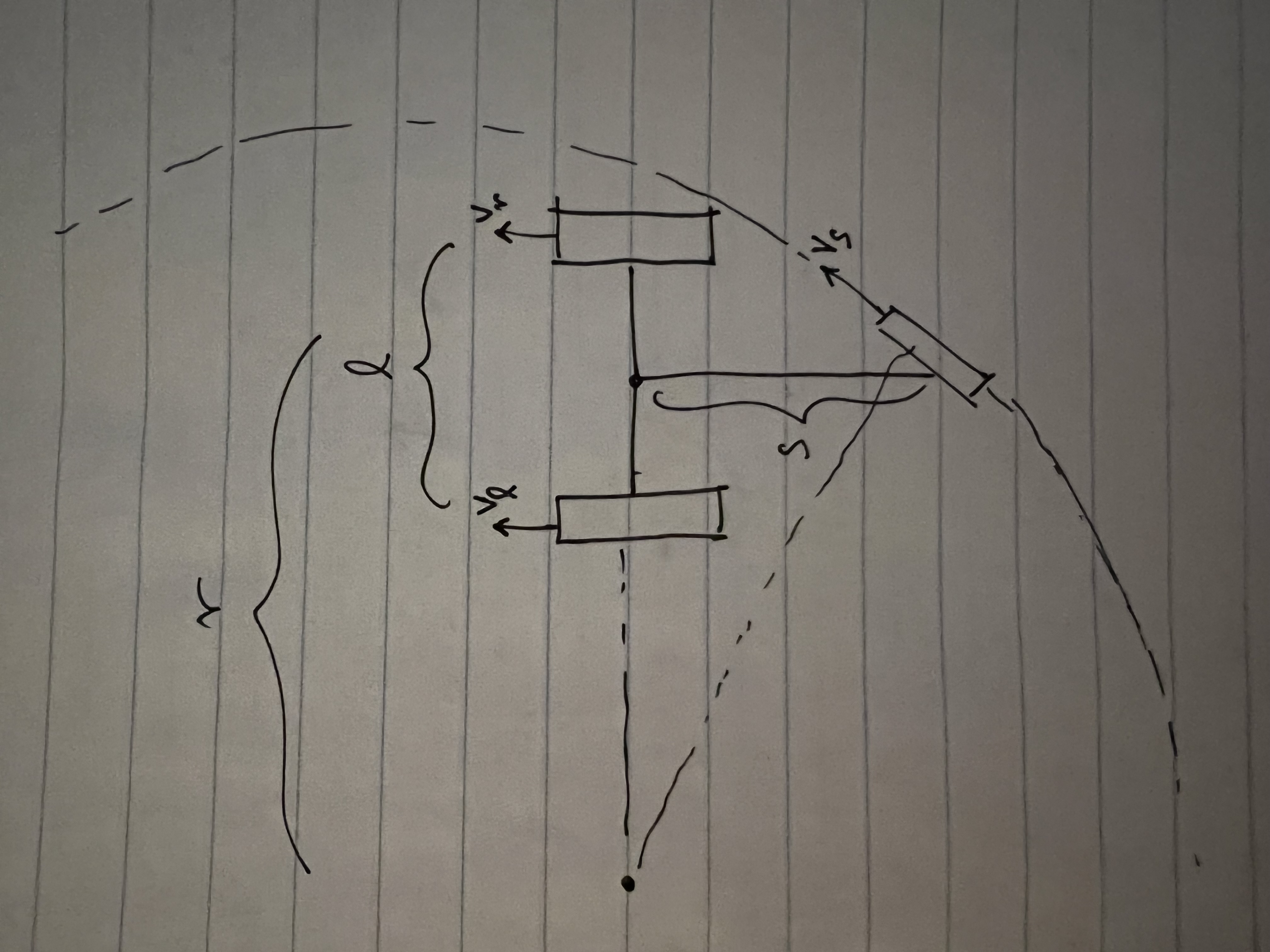
The equation can be applied to the left wheel to derive its inverse
kinematics:
\[\displaylines{\vec{v_l} = \vec{v} + \vec{\omega} \times \vec{r_l} \\ =
\mathbf{v + \omega (r - \frac{l}{2})}}\]
where \(r\) is the turn radius and \(l\) is the width of the robot's front
axle. Applied to the right wheel, the equation yields:
\[\displaylines{\vec{v_r} = \vec{v} + \vec{\omega} \times \vec{r_r} \\ =
\mathbf{v + \omega (r + \frac{l}{2})}}\]
Applied to the swerve wheel, the equation yields:
\[\displaylines{\vec{v_s} = \vec{v} + \vec{\omega} \times \vec{r_s} \\ =
\mathbf{v + \omega \sqrt{r^2 + s^2}}}\]
where \(s\) is the length of the chassis (the distance between the front
axle and swerve wheel).
The angle of the swerve wheel can then be calculated like so using the
geometry of the robot:
\[\displaylines{\theta = \frac{\pi}{2} - tan^{-1}\left( \frac{s}{r}
\right)}\]
Mathematically/intuitively, the equations check out as well. When only
rotating (\(v = 0\)), \(r = \frac{v}{\omega} = \frac{0}{\omega} = 0\), so:
\[\displaylines{ v_l = v + \omega(r - \frac{l}{2}) = \omega \cdot
-\frac{l}{2} \\ v_r = v + \omega(r + \frac{l}{2}) = \omega \cdot
\frac{l}{2} \\ v_s = v + \omega\sqrt{r^2 + s^2} = \omega \cdot \sqrt{ s^2}
= \omega \cdot s}\]
In all three cases, \(v = \omega \cdot r\), where \(r\) is the distance
from each wheel to the "center of the robot", defined as the midpoint of
the front axle. Since rotating without translating will be around a center
of rotation equal to the center of the robot, the previous definition for
\(r\) can be used.
As for the equation for \(\theta\), the angle of the swerve wheel, it
checks out intuitively as well. When only translating (driving straight:
\(\omega = 0\)), \(r = \frac{v}{\omega} = \frac{v}{0} = \infty\), so:
\[\displaylines{ \theta = \frac{\pi}{2} - tan^{-1} \left( \frac{s}{r}
\right) \\ = \frac{\pi}{2} - tan^{-1} \left( \frac{s}{\infty} \right) \\ =
\frac{\pi}{2} - tan^{-1}(0) \\ = \frac{\pi}{2} - 0 \\ = \frac{\pi}{2} }\]
As expected, when translating, \(\theta = 0\), as the swerve wheel must
point straight for the robot to drive straight. When only rotating (\(v =
0\)), \(r = \frac{v}{\omega} = \frac{0}{\omega} = 0\), so:
\[\displaylines{ \theta = \frac{\pi}{2} - tan^{-1} \left( \frac{s}{r}
\right) \\ = \frac{\pi}{2} - tan^{-1} \left( \frac{s}{0} \right) \\ =
\frac{\pi}{2} - tan^{-1}(\infty) \\ = \frac{\pi}{2} - \lim_{x \to +\infty}
tan^{-1}(x) \\ = \frac{\pi}{2} - \frac{\pi}{2} \\ = 0}\]
As expected, when only translating (driving straight), \(\theta =
\frac{\pi}{2}\), or in other words, the swerve wheel is pointed directly
forwards to drive the robot directly forwards. When only rotating,
\(\theta = 0\), or in other words, the swerve wheel is pointed directly to
the right to allow the robot to rotate counterclockwise.
Next Steps:
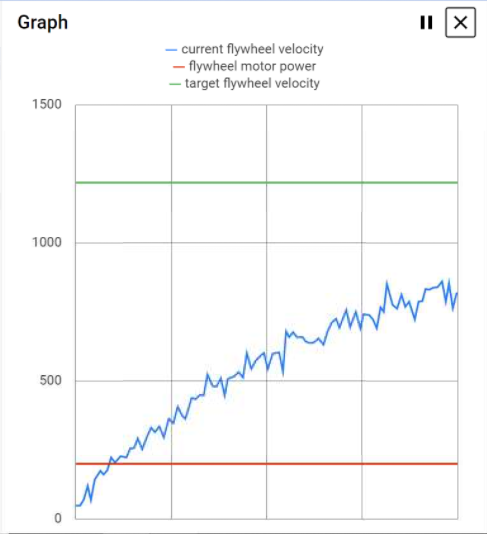
The next step is to use PID control to maintain target velocities and
angles calculated using the derived inverse kinematic equations. Then,
these equations can be used in future motion planning/path planning
attempts to get the robot to follow a particular desired \(v\) and \(
\omega\).
A distance sensor will also need to be used to calculate \(s\), the
distance between the front axle and swerve wheel of the robot.








































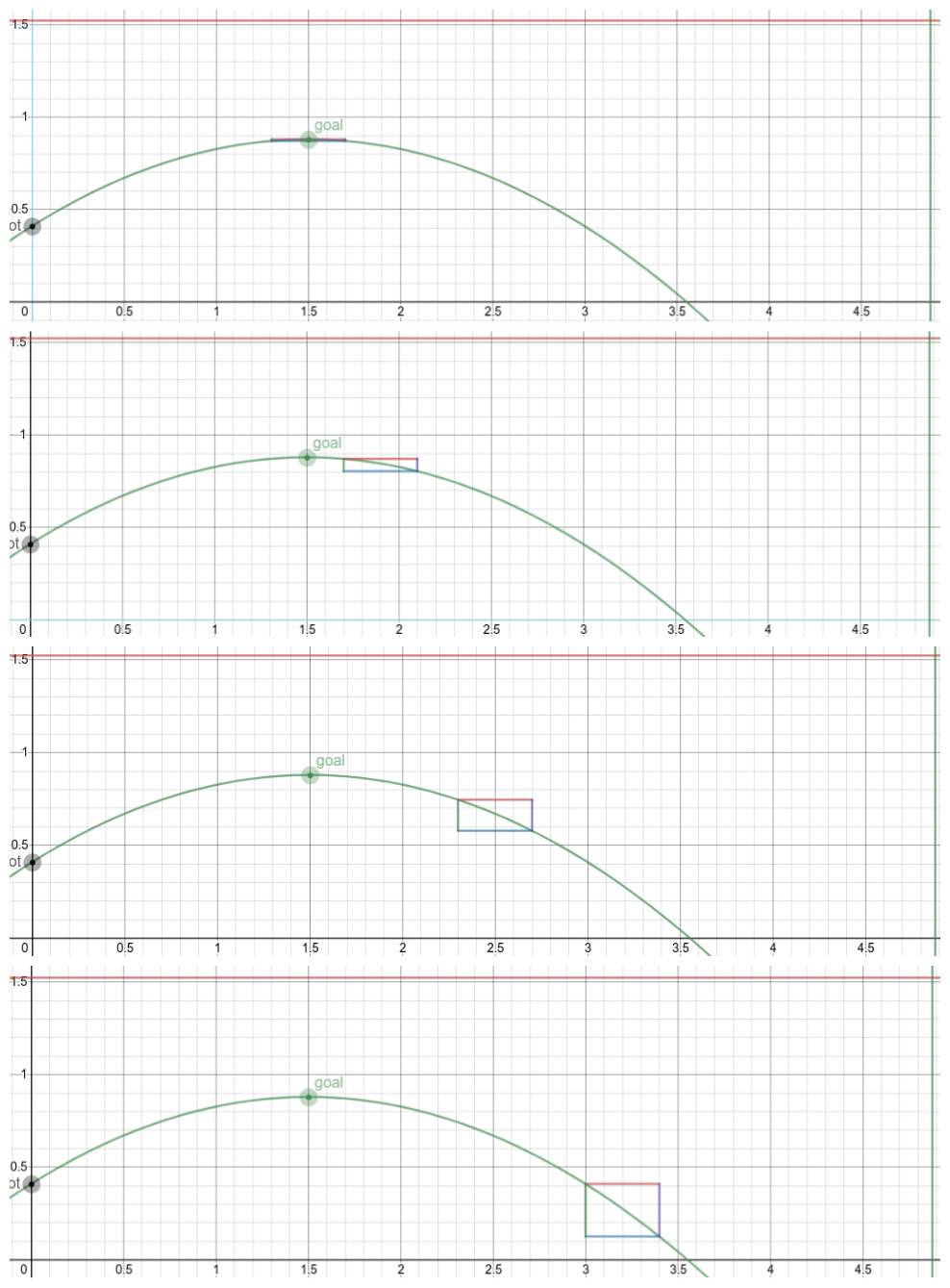






















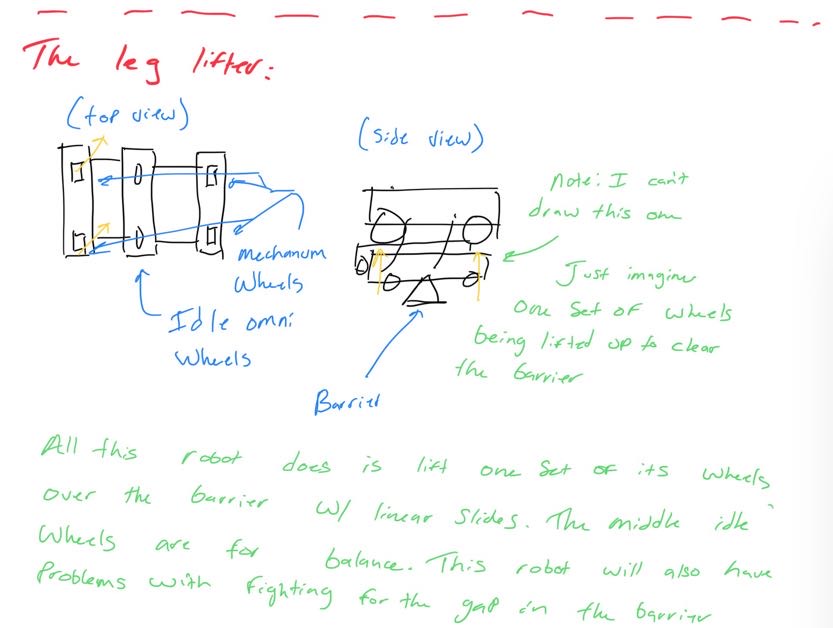
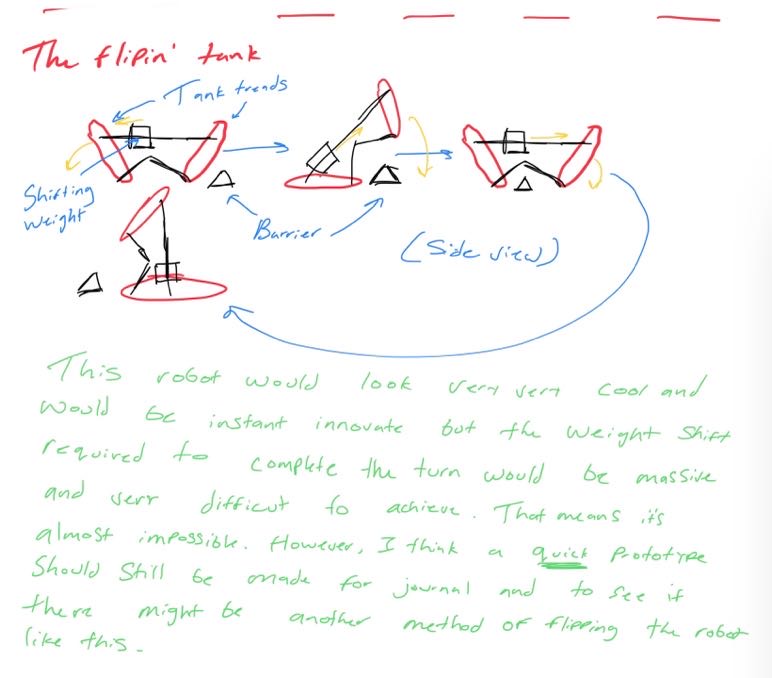













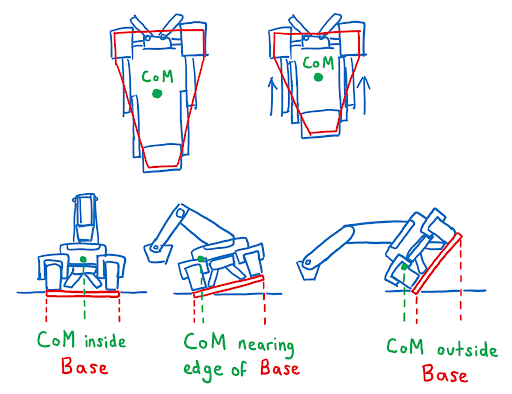 Looking at these diagrams of the robot and its center of mass, we can see how as the crane extends past the base of the robot, the center of mass moves towards the base. Eventually, the center of mass reaches a position outside of the base and the robot falls over. To solve this problem, we would have to either lower the center of mass or limit its fluctuation during movement.
Looking at these diagrams of the robot and its center of mass, we can see how as the crane extends past the base of the robot, the center of mass moves towards the base. Eventually, the center of mass reaches a position outside of the base and the robot falls over. To solve this problem, we would have to either lower the center of mass or limit its fluctuation during movement.
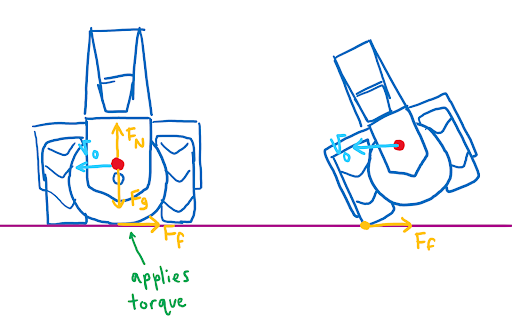
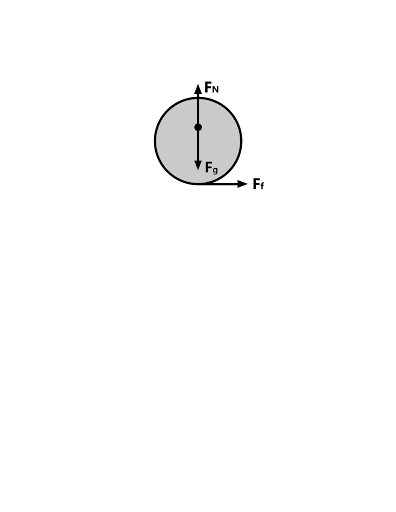 You can see from these free-body diagrams that as we lower the vertical component of the normal force, the overall rotational torque exerted by the swerve module is decreased, which inspired our decisions to lower the center of mass.
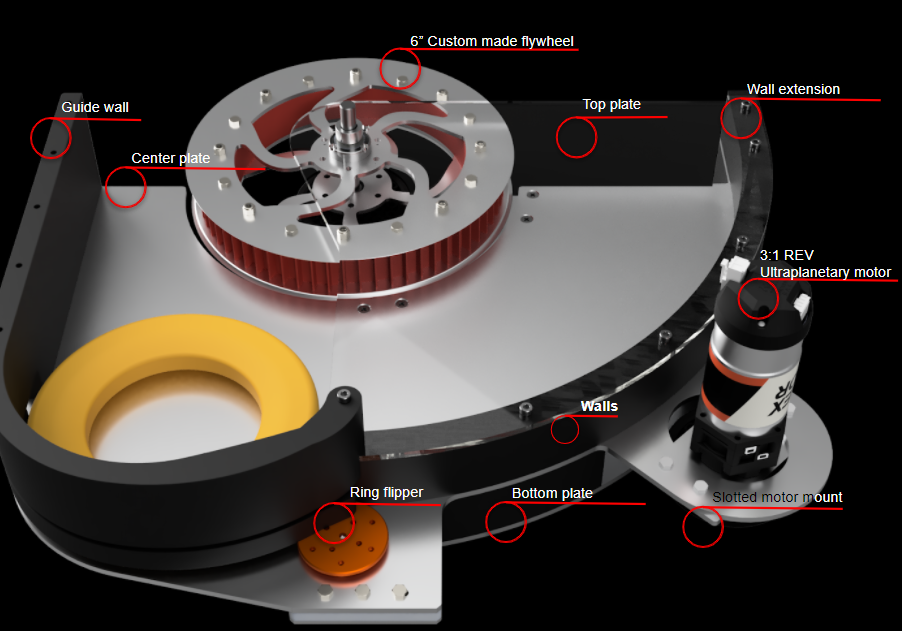
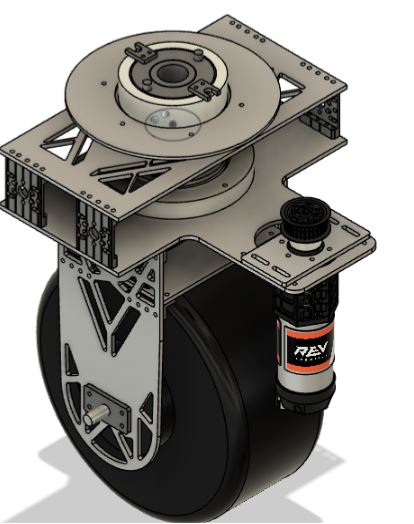
We did this by redesigning our wheel modules and moving the motor further down. Our redesigned wheel modules utilize custom printed "barrier beaters" instead of the rock climbers we used before. These wheels were printed out of ninja flex and nylon and utilized a Gothic Arch design inspired by Monash University's rover wheels. The custom wheel modules used custom carbon-fiber plates and holes in the nylon hub to help reduce weight. Overall, these wheels were excellent at traversing the barriers, weighed less, and the wheel module allowed the motor to drop 5 inches in height. This led to a lower center of mass for the robot.
You can see from these free-body diagrams that as we lower the vertical component of the normal force, the overall rotational torque exerted by the swerve module is decreased, which inspired our decisions to lower the center of mass.
We did this by redesigning our wheel modules and moving the motor further down. Our redesigned wheel modules utilize custom printed "barrier beaters" instead of the rock climbers we used before. These wheels were printed out of ninja flex and nylon and utilized a Gothic Arch design inspired by Monash University's rover wheels. The custom wheel modules used custom carbon-fiber plates and holes in the nylon hub to help reduce weight. Overall, these wheels were excellent at traversing the barriers, weighed less, and the wheel module allowed the motor to drop 5 inches in height. This led to a lower center of mass for the robot.


 However, in the situation that the crane and robot extension did lead to the center of mass nearing the base, we installed an outrigger system as a preventative measure. An outrigger is essentially a beam that extends from a robot that is used to improve stability. Our outriggers used omni wheels and functioned similarly to training wheels, preventing the robot from tipping over when the crane moves out and extends.
However, in the situation that the crane and robot extension did lead to the center of mass nearing the base, we installed an outrigger system as a preventative measure. An outrigger is essentially a beam that extends from a robot that is used to improve stability. Our outriggers used omni wheels and functioned similarly to training wheels, preventing the robot from tipping over when the crane moves out and extends.

 Finally, we implemented some code changes to help deal with this problem, building anti-tipping limiters which allowed for gradual acceleration. This prevented the sudden acceleration mentioned earlier which was a cause of our tipping issue. We also programmed in pre-set arm locations to help keep the center of mass near the wheelbase, making sure that the center of mass never passes the base of the actual robot.
Finally, we implemented some code changes to help deal with this problem, building anti-tipping limiters which allowed for gradual acceleration. This prevented the sudden acceleration mentioned earlier which was a cause of our tipping issue. We also programmed in pre-set arm locations to help keep the center of mass near the wheelbase, making sure that the center of mass never passes the base of the actual robot.